Kappa系数用于一致性检验

也可以用于衡量分类精度

kappa系数的计算是基于混淆矩阵的

kappa计算结果为-1~1，但通常kappa是落在 0~1 间，可分为五组来表示不同级别的一致性：0.0~0.20极低的一致性(slight)、0.21~0.40一般的一致性(fair)、0.41~0.60 中等的一致性(moderate)、0.61~0.80 高度的一致性(substantial)和0.81~1几乎完全一致(almost perfect)。
引自百度百科Kappa系数

公式

k=po−pe1−pe <script type="math/tex" id="MathJax-Element-418">k=\dfrac{p_o-p_e}{1-p_e}</script>

po <script type="math/tex" id="MathJax-Element-419">p_o</script>是每一类正确分类的样本数量之和除以总样本数，也就是总体分类精度

假设每一类的真实样本个数分别为 a1,a2,...,aC <script type="math/tex" id="MathJax-Element-420">a_1,a_2,...,a_C</script>

而预测出来的每一类的样本个数分别为 b1,b2,...,bC <script type="math/tex" id="MathJax-Element-421">b_1,b_2,...,b_C</script>

总样本个数为n

则有： pe=a1×b1+a2×b2+...+aC×bCn×n <script type="math/tex" id="MathJax-Element-422">p_e=\dfrac{a_1\times b_1+a_2\times b_2+...+a_C\times b_C}{n\times n}</script>

例子

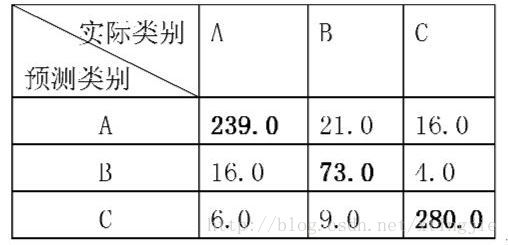
上图就是个混淆矩阵

po=239+73+280664=0.8916 <script type="math/tex" id="MathJax-Element-569">p_o=\dfrac{239+73+280}{664}=0.8916</script>

pe=261×276+103×93+300×295664×664=0.3883 <script type="math/tex" id="MathJax-Element-570">p_e=\dfrac{261\times 276+103\times 93 +300\times 295}{664\times 664}=0.3883</script>

因此：

k=0.8916−0.38831−0.3883=0.8228 <script type="math/tex" id="MathJax-Element-571">k=\dfrac{0.8916-0.3883}{1-0.3883}=0.8228</script>